Perkalian Matriks
- Peserta didik dapat menghitung perkalian dua buah matriks dengan benar
- Peserta didik dapat menghitung perkalian dua buah matriks yang berkaitan dengan kehidupan nyata dengan benar
Setelah kita mempelajari Perkalian Skalar Matriks selanjutnya kita akan belajar Perkalian Matriks. Untuk memahami Perkalian Matriks perhatikan masalah 1 di bawah ini.
Masalah 1
Bu Nani membeli buah mangga dan buah anggur didua tempat yang berbeda. Di Toko buah ke-1, ia membeli 2 kg mangga dan 3 kg anggur, sedangkan di toko buah ke-2, ia membeli 3 kg mangga dan 4 kg anggur. Harga buah mangga dan anggur dikedua toko tersebut sama, yaitu Rp 6.500 dan Rp 10.000 per kg. Berapa banyak uang yang dikeluarkan Bu Nani pada masing-masing toko ?
PenyelesaianUntuk mengetahui banyaknya uang yang dikeluarkan Bu Nani pada masing-masing toko kita dapat menghitungnya sebagai berikut
Toko 1 :
Toko 2 :
Jadi banyak nya uang yang dikeluarkan ibu Nani pada toko ke-1 sebesar Rp 43.000 dan toko ke-2 sebesar Rp 59.500
Untuk menghitung menggunakan perkalian matriks sebagai berikut.
Jumlah buah mangga dan anggur yang dibeli ibu Nani di kedua toko tersebut dapat dibentuk ke dalam tabel sebagai berikut.
| Buah Mangga | Buah Anggur | |
|---|---|---|
| Toko 1 | 2 | 3 |
| Toko 2 | 3 | 4 |
Jika bagian angka pada tabel dituliskan dalam bentuk matriks, misalkan matriks
Selanjutnya harga kedua macam barang yang dibeli Bu Nani dapat disajikan dalam bentuk tabel sebagai berikut
| Nama Barang | Harga |
|---|---|
| Buah Mangga | 6.500 |
| Buah Anggur | 10.000 |
Jika tabel harga kedua barang dimisalkan kedalam bentuk matriks yaitu matriks
Dengan demikian uang yang dikeluarkan Bu Nani untuk masing-masing toko dapat dinyatakan sebagai perkalian matriks P dan matriks Q sebagai berikut.
Jadi hasil perkalian matriks dan matriks mendapatkan matriks baru yang merupakan uang yang dikeluarkan Bu Nani untuk masing-masing toko.
Dari contoh diatas, kira memperoleh matriks berodo dan matriks berodo , sedangkan matriks hasil Perkalian berodo . Dapat ditarik kesimpulan pengertian Perkalian Matriks Sebagai berikut.
Dua buah matriks dan dapat dikalikan, jika banyak kolom pada matriks sama dengan banyaknya baris pada matriks . Elemen-elemen pada matriks dapat diperoleh dari Penjumlahan hasil kali elemen baris pada matriks dengan elemen kolom pada matriks . Dapat digambarkan sebagai berikut
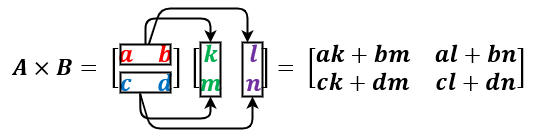
Agar lebih memahami perhatikan masalah 2 di bawah ini.
Masalah 2
Sebuah perusahaan travel bus ingin membuka cabang baru didua kota, cabang 1 di kota Banjarmasin dan cabang 2 di kota Samarinda. Untuk itu diperlukan beberapa peralatan sebagai penunjang kelancaran usaha tersebut, yaitu handphone dan komputer. Disisi lain perusahaan mempertimbangkan harga satuan peralatan tersebut. Lengkapnya disajikan pada tabel dibawah.
| Handphone (Unit) | Komputer (Unit) | |
|---|---|---|
| Cabang 1 (Banjarmasin) | 4 | 3 |
| Cabang 2 (Samarinda) | 5 | 4 |
| Nama Barang | Harga (Rp) |
|---|---|
| Handphone | 1.500.000 |
| Komputer | 5.450.000 |
Perusahaan ingin mengetahui biaya yang dikeluarkan tiap cabang. Hitunglang menggunakan perkalian matriks.
PenyelesaianUntuk menghitung kedalam bentuk matriks kita misalkan tabel pertama sebagai matriks dan tabel kedua sebagai matriks .
- Isilah inputan di bawah ini berdasarkan pernyataan diatas.
- Inputkan jawaban tanpa titik.
- Tekan tombol cek untuk mengecek jawaban.
- Apabila inputan berwarna Hijau jawaban benar, apabila inputan berwarna Merah jawaban salah.
| [ |
|
] |
| [ |
|
] |
Agar lebih memahami Perkalian matriks, perhatikan contoh berikut.
Contoh
Diketahui matriks , , dan . Tentukan :
Cek Pemahaman Anda
-
Diketahui matriks dan . Hitunglah .
[
] -
Diketahui matriks dan . Hitunglah
[
]